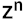How to use Fractal Generator
| Click anywhere in the image to zoom in at the current cursor position by the
zoom
increment amount. |
| Click, drag and release to zoom into drawn area. |
| Ctrl + Click to zoom out at current cursor position by zoom increment amount.
|
| Shift + Click to centre at current cursor position. |
| Alt(Option) + Click to toggle between Mandelbrot and Julia modes at current
cursor position (useful points of interest can be found just outside the perimeter of the Mandelbrot set).
|
 |
Reset to default settings. |
 |
Zoom in. |
 |
Zoom out. |
 |
Turn zoom animation on/off. |
 |
Cycle modes (Mandelbrot, Julia). |
 |
Cycle variants (Standard, Burning Ship, Tricorn). |
 |
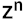Cycle exponent (integer 2-6). |
 |
Cycle colot theme. |
 |
Shift color theme up. |
 |
Shift color theme down. |
 |
Rotate Julia set clockwise. |
 |
Julia set anti-clockwise. |
 |
Turn Julia spin animation on/off. |
 |
Save current image. |
 |
Open/close settings panel. |
 |
Open/close help panel. |
Creating Custom Color Gradients
- Choose a palette depth of 4, 8, 12 or 16 colors.
- Choose a gradient depth of 16, 32, 64, 128, 256 or 512 levels.
- Choose the color interpolation method ('None' or 'Linear').
- Create the palette by picking colors using the color picker widget and applying the selection to each
palette slot in turn.
- Click 'PAINT'. A color gradient will be created dynamically and applied to the displayed fractal.
- The custom color gradient will also be added to the list of available color rendering themes in the format
'User_x_nnn', where 'x' is an auto-incremented number and 'nnn' is the number of levels.
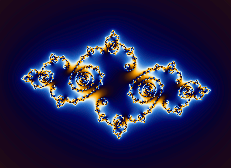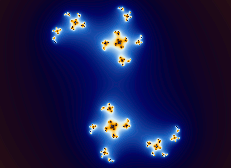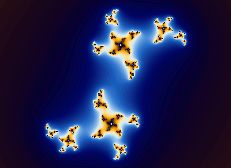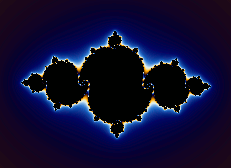
Navigating Mandelbrot and Julia Sets
The Mandelbrot set can be considered a map to an infinite number of Julia sets. Pressing
Alt(Option) + Click or at various points around the
Mandelbrot set (or its variants) produces a variety of
Julia sets. The most interesting images can be found just outside the perimeter of the Mandelbrot set.
Mandelbrot variants like the so-called 'Burning Ship' can map to extraordinarily beautiful Julia sets.
Julia sets can be 'rotated' about their origin by applying a polar rotation transformation to the
complex coordinate c in the equation z = zⁿ + c. By successively incrementing the rotation angle by pressing
the button, a 'spinning Julia' animation can be
produced.
The frame rate or speed of rotation is governed by the 'Spin Inc' setting; smaller values produce slower and
more intricate rotations.
